视觉SLAM十四讲读书笔记：Ch05相机与图像

这是我系列博客《视觉SLAM十四讲》的读书笔记中的一篇，总结了第五章“相机与图像”的内容。

1 相机模型

1.1 针孔相机模型

使用小孔成像来类比针孔相机模型：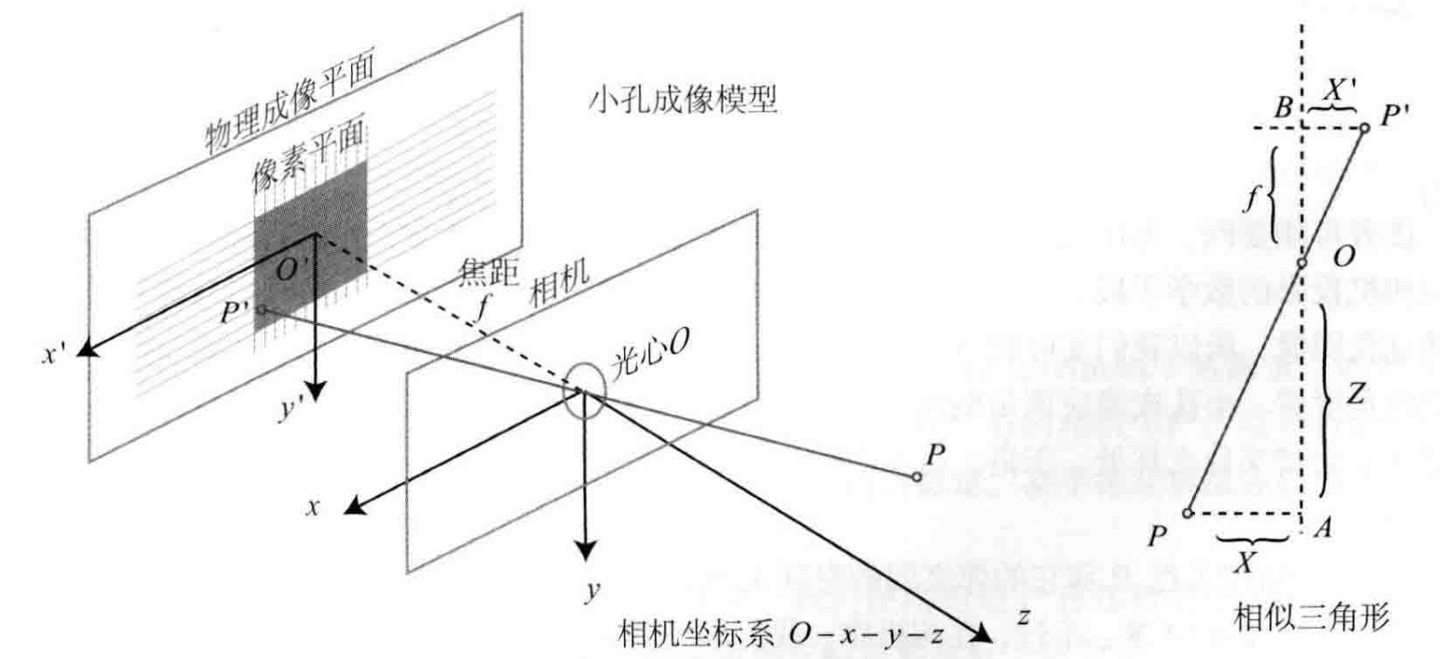

我们有两个坐标系：

1. 以光心为原点的相机坐标系，光心用小孔来类比
2. 物理成像平面坐标系，其平行于相机坐标系的平面并且距离为焦距

两个坐标系都是以向右为x轴正方向、向下为y轴正方向（参考使用opencv时的索引方法）

对于真实的物体和成像点，根据三角形相似关系得到： 式子中有负号是因为小孔成像成的是倒像。我们将成像平面对称地放置在相机前方

image-20250810184712065

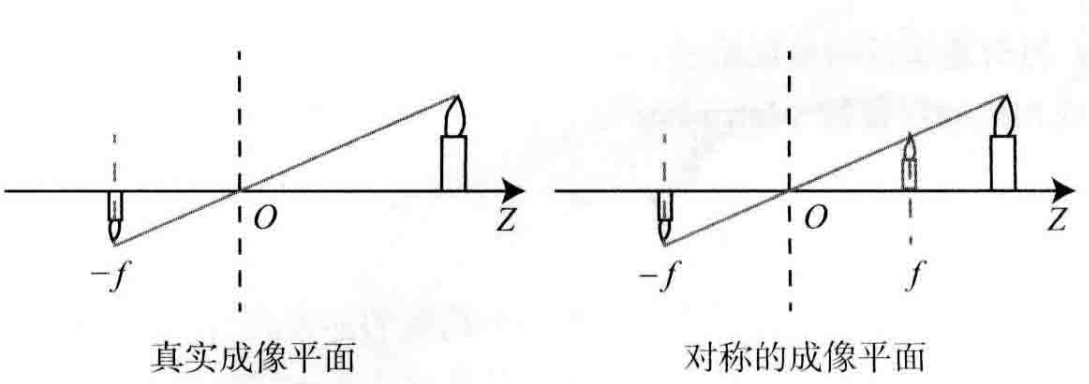
这样式子就变成了： 这样我们得到了从真实世界坐标系到成像平面坐标系的转换： 为了得到我们最终的像素坐标系，我们还需要在成像平面上进行采样和量化，得到像素坐标系

根据我们上面的描述，显然从成像平面到像素平面的过程需要缩放。同时，我们处理的图像的像素索引是没有负数的，因此还需要平移，我们可以把像素坐标与相机坐标系、成像平面坐标系的关系描述为： 其中，单位为像素。

转换为齐次坐标，得到： 习惯性地，我们将上式描述为： 我们由此定义了相机的内参矩阵。我们可以通过标定来确认这个矩阵。

在上式中，我们使用的P是相机坐标，但是我们通常知道的是世界坐标，因此我们需要相机的位姿来描述，相机的位姿由旋转矩阵R和平移向量t来描述： 注意在上式中隐式地包含了一次齐次坐标到非齐次坐标的转换（我们使用TP来描述位姿变换）。

在上式中，描述了世界坐标系到相机坐标系的投影关系，其中的称为相机的外参，不同于内参始终不变，外参会随机器人轨迹变化，是我们SLAM问题中待估计的目标之一。

从另一个角度来看，我们由式子可以知道这个过程相当于先将世界坐标系的点转换到相机坐标系，再除去最后一维（深度）数值，得到了点P在归一化平面上的投影： 上式最后的归一化坐标可以看成是相机前方z=1处平面上一点，这个z=1平面称为归一化平面。如果对相机坐标同时乘以一个数，归一化坐标是一样的，说明这个点的深度信息丢失了，所以单目相机没法得到像素点的深度信息。

1.2 畸变模型

相机的透镜可能会对成像产生影响。

由透镜形状引起的畸变（Distortion）称为径向畸变，分为两大类：桶形畸变和枕形畸变。

image-20250813184059624

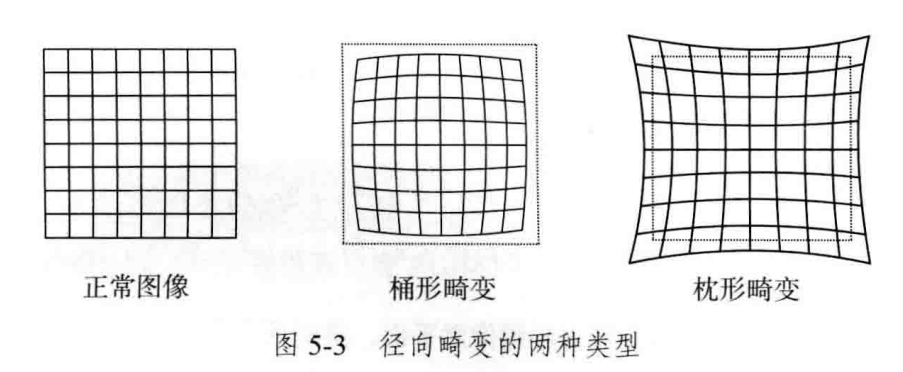
桶形畸变图形放大率随着与光轴的距离增加而减小，而枕形畸变相反。在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。

透镜组装与成像面没能严格平行，会引入切向畸变。可以看成坐标点沿着切线方向发生了变化，也就是水平夹角（极坐标描述）发生了变化。

image-20250813184319080

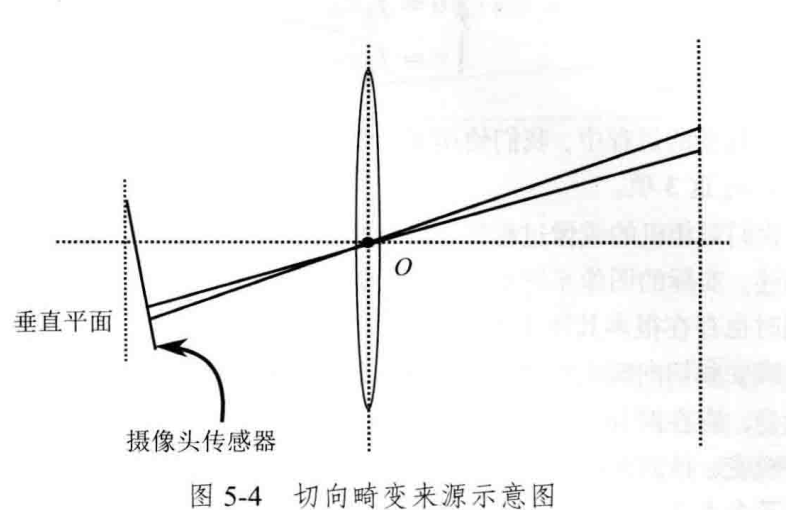
为了描述径向畸变和切向畸变，对于归一化平面上的坐标为的点，其极坐标为。通常假设畸变呈多项式关系： 其中为畸变后点的归一化坐标。气象畸变可以使用另外两个参数进行纠正： 综上所述，我们可以使用五个畸变系数来找到点畸变后在像素平面上的正确位置：

1. 将三维空间点投影到归一化图像平面，得到归一化坐标
2. 对归一化平面上各点计算径向畸变和切向畸变

3. 将畸变后的点通过内参矩阵投影到像素平面：

一般来说，我们会对整张图象进行去畸变，然后根据去畸变的图像讨论此图像上的点的空间位置。

最后我们总结单目相机的成像过程

1. 世界坐标系下点P坐标为
2. 相机的运动使用描述，得到相机坐标系下点坐标为
3. 对归一化到平面上得到
4. 根据畸变参数对进行去畸变
5. 经过内参得到像素坐标

1.3 双目相机模型

单目相机无法确定深度，因此单目相机成像后，像素坐标对应的可能的相机坐标是一条直线：

image-20250813205340327

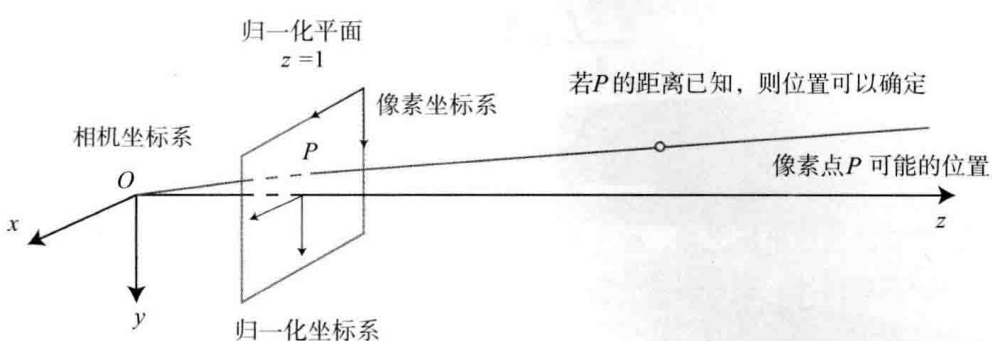
双目相机类似于人眼，同步采集左右相机的图像，计算图像间视差，估计每一个像素的深度。

image-20250814210125941

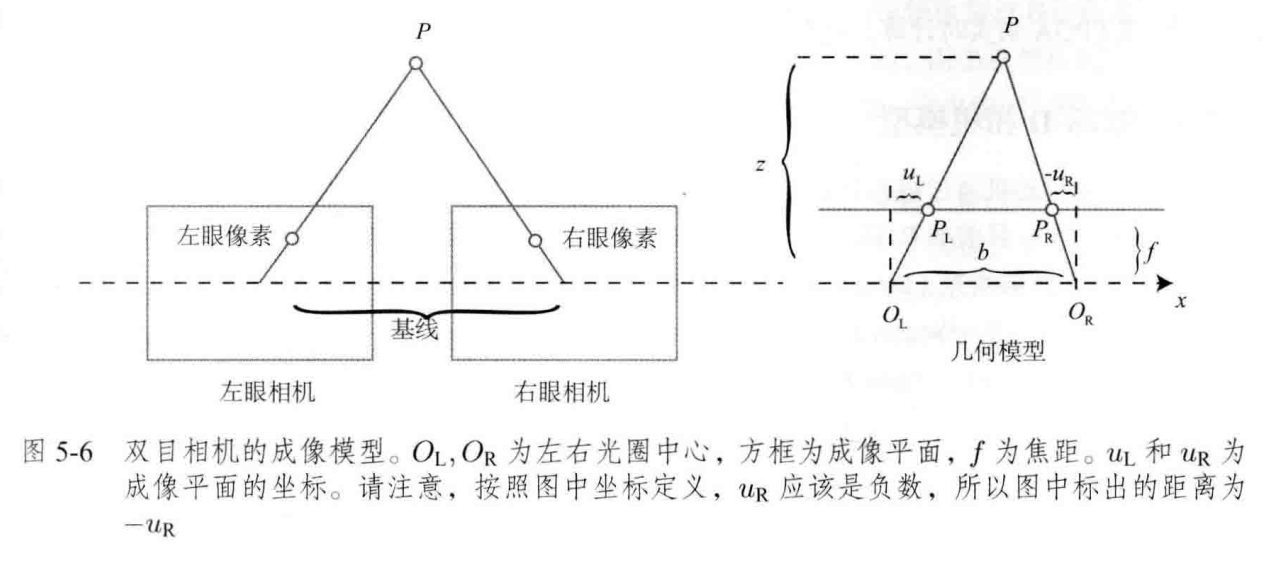
我们将两个相机都视为针孔相机，水平放置，光圈中心都在x轴上，两个光圈的距离称为基线，记作。

考虑空间点，在左右眼相机中成的像分别为。理想情况下，两个相机只有x轴上的差异，所以P也只在x轴（图像的u轴）上有差异，记两像坐标为和，根据和的相似关系可以知道 整理得 其中定义为视差。通过视差我们就能计算深度。视差与深度成反比，由于视差得最小单位为一个像素，于是双目相机的深度存在一个理论最大值，由确定，基线越长，双目相机测得的最大距离就越远。

虽然视差计算公式很简洁，但是实际计算困难，因为我们不知道左眼图像的某个像素出现在右眼图像中的哪个位置。

1.4 RGB-D相机模型

RGB-D相机按照原理可以分为两大类

1. 结构光（Structured Light）：通过投射特定红外光图案并捕捉其在物体表面的变形，计算深度信息（如 Kinect 1、Intel RealSense）。
2. 飞行时间（ToF, Time-of-Flight）：通过测量光脉冲从发射到返回的时间来计算距离（如 Kinect 2、ToF 传感器）。

无论哪种方式，RGB-D 相机都会主动发射光（通常是红外光）获取深度，与 RGB 摄像头结合可生成三维彩色点云。结构光适合精度较高的近距离测量，而 ToF 更适合快速获取较大场景的深度信息。

2 图像

数学中，图像可以由一个矩阵来描述；在计算机中，可以用二维数组描述。以最简单的灰度图为例子，在一张灰度图里面，每个像素的位置对应一个灰度值，所以一张宽度为、高度为的图像在数学上可以记作一个函数 其中为坐标。常见的灰度图中可以用0到255的整数（unsigned char）来表达灰度读数，那么一张宽度为640像素、高度为480像素的灰度图像可以表示为

unsigned char iamge[480][640]

在程序中图像以二维数组的形式存储，图像的列对应X轴（宽）、图像的行对应Y轴（高）。按照上述定义方式，一个位于处的像素，对应访问方式为：

unsigned char pixel = image[y][x]

对于更加复杂的图像，有的需要采用16位整数来记录，有的则需要多个通道。