视觉SLAM十四讲读书笔记：Ch04李群与李代数 (1)

Posted on In Views:

这是我系列博客《视觉SLAM十四讲》的读书笔记中的一篇，总结了第四章“李群与李代数”中有关李群和李代数的定义、转换等基础知识的内容

img

1. 李群（Lie Group）与李代数（Lie Algebra）基础

1.1 群与李群

群的定义：

一个群 是一个集合，配备有一个满足以下条件的二元运算 ：

  • 封闭性：若 ，则
  • 结合律：
  • 单位元存在：存在单位元 ，使得
  • 逆元存在：每个 ，存在 ，使得

李群的定义：

李群（Lie Group） 是兼具群结构与光滑流形结构的集合。也就是说，群运算 在微分意义上是可导的（smooth）。

经典例子包括：

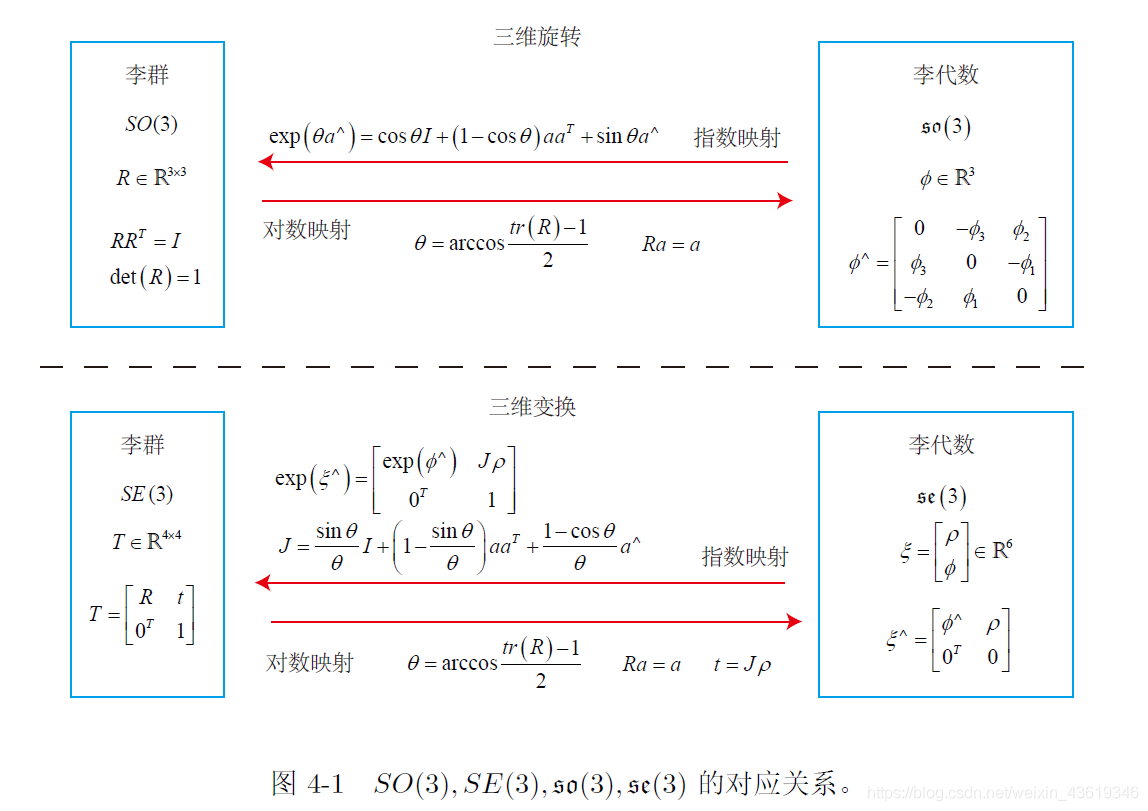
  • ：三维空间旋转群
  • ：三维空间欧氏变换群（旋转 + 平移）

注意：SO(3)、SE(3) 并不在加法下封闭，不能使用向量加法来组合两个旋转/位姿。

2. 从李群引出李代数

2.1 SO(3) 的李代数引出

SO(3) 的定义是： 对等式 对时间求导： 乘以 （或 ) 得： 是反对称矩阵 定义： 这是 SO(3) 在单位元处的切空间（李代数） 的定义方式之一，表明旋转矩阵的“导数”信息可以由一个三维向量表示。

2.2 李代数（Lie Algebra）的定义

一个李群 GG 对应一个李代数 ，是其在单位元附近的切空间，配备有一个称为 李括号（Lie Bracket） 的运算 ，满足：

  • 双线性（bilinear）
  • 反对称性：
  • 雅可比恒等式：

例如，三维向量叉乘就是一种李括号：

2.3 SO(3) 的李代数

记号说明：

  • 李群：
  • 李代数：，由所有反对称 实矩阵组成。

定义： 我们使用“帽子运算”将三维向量与反对称矩阵对应： 其李括号定义为：

2.4 SE(3) 的李代数

从 SE(3) 的定义出发： 类似地，对 求导，可以得到： 其中： 李括号为：

3. 指数映射与Rodrigues公式

3.1 SO(3) 上的指数映射

指数映射定义为： 我们使用泰勒展开： 设 ，其中 是旋转轴， 是旋转角度。 可得： 这就是Rodrigues 公式，说明李代数和旋转的角轴表达形式其实等价的。

3.2 对数映射

对数映射是指数映射的逆： 使用幂级数展开： 需要注意：

  • 指数映射是满射（surjective）：每个 都可以表示为某个李代数元素的指数
  • 但不是单射（injective）：因为 和 映射结果相同

3.3 SE(3) 上的指数映射

设： 指数映射： 其中称为 左雅可比矩阵，表示平移部分的积分：

推导如下，仍然使用：

4. 总结

img