数据结构：划分树

Posted on Edited on In Views:

施工中，未完待续...

引入

划分树是一种来解决区间第 大的一种数据结构，其常数、理解难度都要比主席树低很多。同时，划分树紧贴「第 大」，所以是一种基于排序的一种数据结构。

在学习划分树之前，建议各位可以先了解主席树，笔者计划在之后的博客中也会介绍

过程

建树

划分树的建树比较简单，但是相对于其他树来说比较复杂。

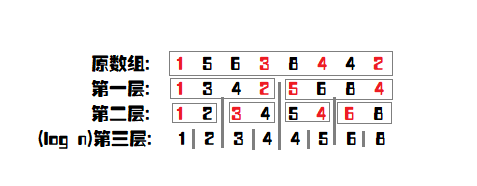
如图，每一层都有一个看似无序的数组。其实，每一个被红色标记的数字都是 要分配到左儿子的。而分配的规则是什么？就是与 这一层的中位数 做比较，如果小于等于中位数，则分到左边，否则分到右边。但是这里要注意一下：并不是严格的 小于等于就分到左边，否则分到右边。因为中位数可能有相同，而且与 的奇偶有一定关系。下面的代码展示会有一个巧妙的运用，大家可以参照代码。

我们不可能每一次都对每一层排序，这样子不说常数，就算是理论复杂度也过不去。我们想，找中位数，一次排序就够了。为什么？比如，我们求 的中位数，其实就是在排完序过后的 num[mid]。

两个关键数组：

tree[log(N),N]: 也就是树，要存下所有的值，空间复杂度 。 toleft[log(N),n]: 也就是每一层 1~i 进入左儿子的数量，这里需要理解一下，这是一个前缀和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void Biuld(int left, int right, int deep){
    int i, mid, ls, rs, flag, same;//其中flag用于平衡两边数量
    if(left==right){
        return;
    }
    mid = (left+right)/2;
    same = mid-left+1;
    for(i=left;i<=right;i++){
        if(tree[deep][i] < num[mid])
            same--;
    }
    ls = left;
    rs = mid+1;
    for(i=left;i<=right;i++){
        flag = 0;
        if((tree[deep][i]<num[mid])||(tree[deep][i]==num[mid]&&(same>0))){
            flag =1;
            tree[deep+1][ls] = tree[deep][i];
            ls++;
            if(tree[deep][i]==num[mid])
                same--;
        }
        else{
            tree[deep+1][rs]=tree[deep][i];
            rs++;
        }
        toleft[deep][i] = toleft[deep][i-1] + flag;
    }
    Build(left,mid,deep+1);
    Build(mid+1,right,deep+1);
    return;
}